数学コラムの目次
今日の数学問題#220

今日の数学コラム
因数分解の導入部分で重要なのは素因数分解です。
素因数分解は中学1年生で学ぶのですが、ここを理解しておかないと因数分解を理解したことにはならないのできちんと復習しておきましょう!
これであなたも素因数分解マスターです!
因数とは
1つの式や数を分解して積の形にした時の各要素の事を言います。
例えば、30=5×6
この場合は5と6を因数と言います。
それを文字で表すと

この場合
因数はaと(x+y)になります。
特に左辺のaはax,ayどちらにも含まれているので共通因数と言います。
素数とは
2以上の自然数で正の約数が1と自分自身のみである数字のことです。
例えば、13は1と13しか約数はありませんので素数となります。
4は1,2,4が約数なので素数ではありません。
素数の研究は進められていて、現時点で2を8258万9933回かけた数から1を引いた数が判明している最大の素数と言われています。
また、よくある問題として「1」は素数なのか?というのがあります。
定義にあるように2以上を素数とするので1は素数ではありません。
【問題】
次の数字の中から素数を選びましょう!
1,11,42,51,73
【答え】
11,73
素因数分解とは?
素因数分解とは、ある数を素数のかけ算で表すことです。
因数はかけ算に表記したものなので、無数に出てきてしまいますよね。
例えば36を分解すると6×6、2×18,3×12など全て因数です。
素因数分解では
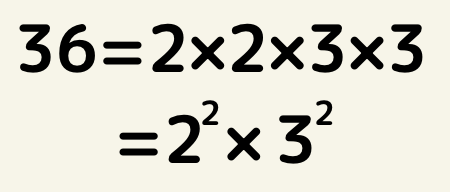
簡単にいえば分解できないところまで徹底的にやりましょう!と覚えてもらえれば良いです。
素因数分解のやり方
108を素因数分解しましょう。
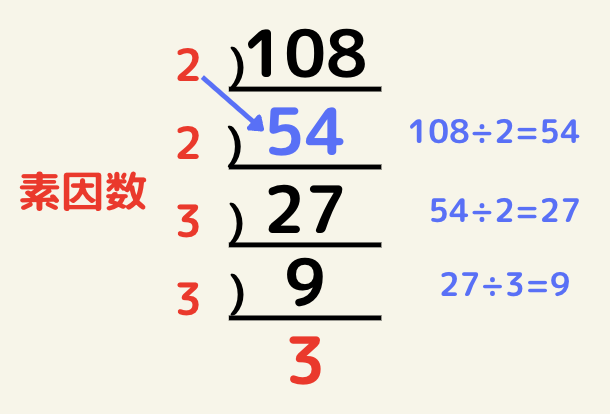
手順はとしては、
1.108の一の位が偶数なのでとりあえず2で割る
2.54の一の位が偶数なのでとりあえず2で割る
3.27は各位を足すと3の倍数になるので3で割る
4.9は3の倍数なので3で割る
見極めるポイントとしては、
★一の位が偶数→2で割れる
★一の位と十の位が00→4で割れる
★一の位が0か5→5で割れる
この場合だと108=2×2×3×3×3=2^2×3^3
が答えになります。
入試問題にチャレンジ!
2けたの正の整数XとYがある。整数Xは十の位の数がa,一の位の数がbであり,整数Yは,十の位の数がb,一の位の数がaである。ただし,a<bとする。このとき,(1)〜(4)に答えなさい。
(1)2つの整数XとYの積XYをa,bを用いて表しなさい。
(2)ab=6,a^2+b^2=37のとき,積XYの値を求めなさい。
(3)(2)のとき、整数Xを求めなさい。
(4)積XYが2268のとき,整数Xを求めなさい。
(出典:2015年 佐賀県)
【解答】
(1)X=10a+b,Y=10b+aなので、(10a+b)(10b+a)=100ab+10a^2+10b^2+ab=10a^2+101ab+10b^2
(2)XY=10(a^2+b^2)+101ab=10×37+101×6=370+606=976
(3)976を素因数分解すると

だから976=2^4×61
a<bだからX<Yなので、X=16
(4)2268を素因数分解すると、
2268=2^2×3^4×7
つまり、素因数に7が含まれている2桁の整数の組み合わせを考える。
X→Y
(i)7×2=14→41
(ii)7×3=21→12
(iii)7×2×2=28→82
(iv)7×2×3=42→24
(v)7×3×3=63→36
(vi)7×2×2×3=84→48
この時入れ替えた数には素因数として3が必ず含まれているはずであるので、(iv)(v)(vi)のいずれかになる。
また、a<bだからX<Yなので、(v)を考えると、
36=2^2×3^2なので、X=36が答えになる。
※念の為確認しよう!
63×36=(7×3^2)×(2^2×3^2)=2^2×3^4×7=2268なので問題なし!
この難易度なら(1)〜(3)までできればOK!
(4)は高校入試だけでなく、大学入試でも良く出てくるパターンです。
数学は定理を使って解くことに慣れてしまうとこのように実験をしてとにかく数字を当てはめてみると言う解き方がひらめかなくなってしまいます。
このパターンは出来るだけ条件を絞って仮に数字を当てはめて考えてみるのが定石です。
以上!京都市中京区のアイデア数理塾、油谷がお届けいたしました!
今日の数学 解答#220



