数学コラムの目次
京の算数学問題#189

アイデア数理塾はこちら
算数学コラム
1次方程式と連立方程式のフォルムの違い
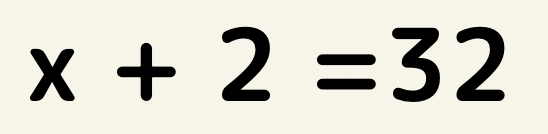
これが、中学1年生で学ぶ1次方程式です。
文字の種類が1種類で式の次数が1なので、1元1次方程式と言います。
一方で、連立方程式は、
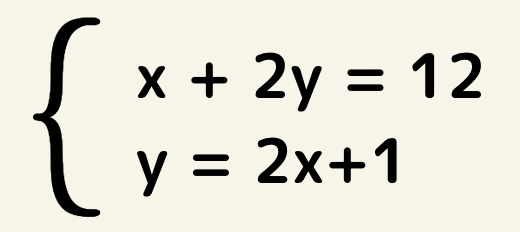
2つの1次方程式が連なった形をしています。
そして2つの種類の文字があります。
つまり2元1次方程式を2つ連ねた形が中学2年生で学ぶ連立方程式です。
これが1番大きなフォルムの違いです。
解の考え方の違い
方程式はxの値を求めるというシンプルな解釈になりますが、
連立方程式は2つの式が共通の解(同じx,y)を持つと仮定した上でx,yの値を求めるという前提が入ります。
また、グラフ上で表すと、方程式は数直線で表し、連立方程式は1次関数の2本のグラフの交点です。
どう使い分けるのか?
中学の定期テストの問題だと文章題は比較的わかりやすい問題が多いです。
例えば、りんごとみかん2つを○個買った。りんごは1つ□円、みかんは1つ△円で支払った合計金額は○○円だった。
という文章題の場合、りんごとみかんという2つの指標が出てくるのでx,yという2つの文字を使う必要があるとわかり、①りんご+みかんの合計数、②りんごの金額+みかんの金額という2つの式を立てることができる。
ただ!
この問題は方程式でも解くことが出来ますよね。
なので定期テストで意識すべきはどの単元が出題されているか?を理解することです。
正直、文章題は連立方程式でも方程式でもどちらでも解くことが出来ますが、問題文で連立方程式で解きましょうとか、りんごをx個、みかんをy個とした時にとか前提条件が問題文にある場合は迷わず連立方程式を使いましょう!
鶴亀算をいろんな解き方で解いてみた
鶴と亀が合わせて35匹いる。足の合計は110本でした、鶴と亀はそれぞれ何匹いますか?
その1 全部鶴と仮定して解いてみた
全部鶴と仮定すると鶴は足が2本なので、2本×35匹=70本 の足がある。
ですが合計は110本なので、110-70=40本足りないことになる。
ここで鶴を亀に変えて考える。
鶴を亀に変えた場合足の数は2本ずつ増えるので、40本増やすためには
40÷2=20匹亀と入れ替えれば良い。
よって鶴は15匹、亀は20匹
その2 1次方程式で解いてみた
鶴をx匹とすると亀は(35-x)匹である。
つまり、足の合計数に関して方程式を立てると
2x + 4(35-x)=110
x=15
亀は35-x=35-15=20
よって鶴は15匹、亀は20匹
その3 連立方程式で解いてみた
鶴をx匹、亀をy匹とすると、
全体の合計匹数
x + y = 35
全体の足の数
2x + 4y = 110 の2つの式が立てられる。
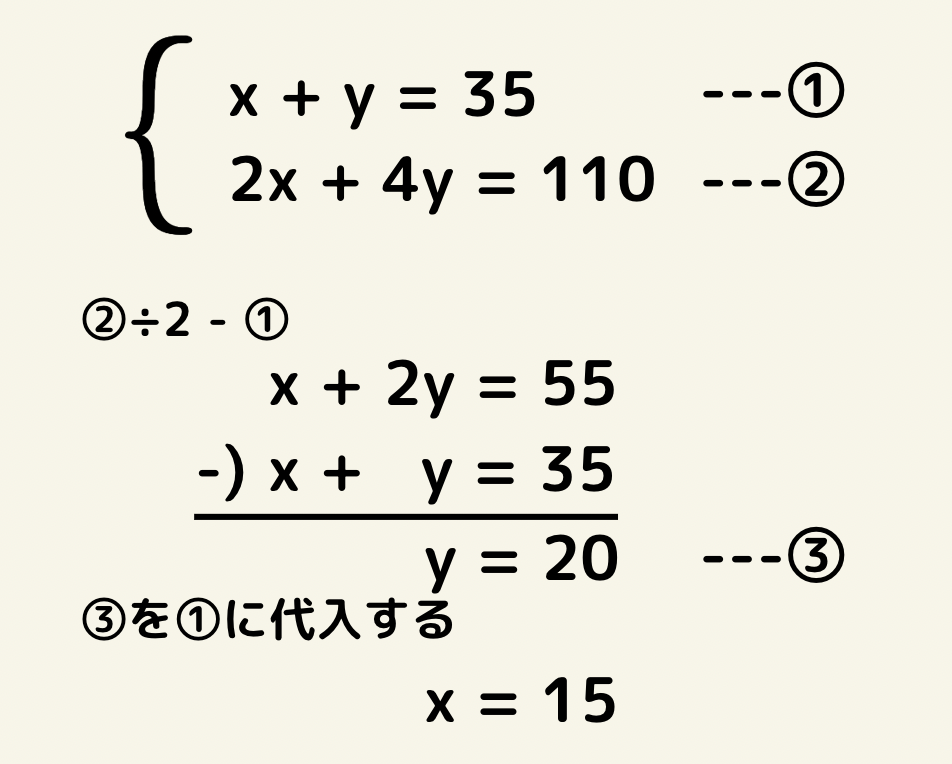
よって鶴は15匹、亀は20匹と言える。
個人的には連立方程式の方が解きやすいと感じたのですが皆さんはどうでしょうか?
慣れてくると一次方程式か連立方程式か判断する基準は「いかに楽に解くことができるか?」を基準にすると良いです。
慣れてくるまではひたすら問題を解く!
案外シンプルですがこれが一番効きます^^
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#189

元は文字の種類、次は式の次数のことです。
この場合文字はyとxの2種類であり、式の次数は1次式なので2元1次方程式となる。



