数学コラムの目次
京の算数学問題#186

算数学コラム
連立方程式って初めてみた時はこんなの解けるの?なんて思うかもしれませんがやり方さえ覚えれば入試の得点源になったりします。
特に京都の公立高校数学の入試問題では、大問1をいかに取るか?がキモになってきます。
だいたい偏差値50前後以上の学校を目指すのであればここが勝負の分かれ道にもなり得ますのでしっかり確認しておきましょうね^^
下記に連立方程式の解説を載せていますので一番下のリンクから見てみてくださいね^^
3元1次方程式
中学2年生で習う連立方程式は2元1次方程式でした。
元は文字の種類、次は式の次数でしたね!
例えば
3a + 2b = 5 これが2元(a,bの2種類)、1次(多項式の次数が1)方程式になります。
ではこれが高校数ⅠAの範囲になると
3元1次方程式になるのです!
文字が3種類の連立方程式を解くという事です。
では早速問題を考えてみましょう!
3つの連立方程式の解き方
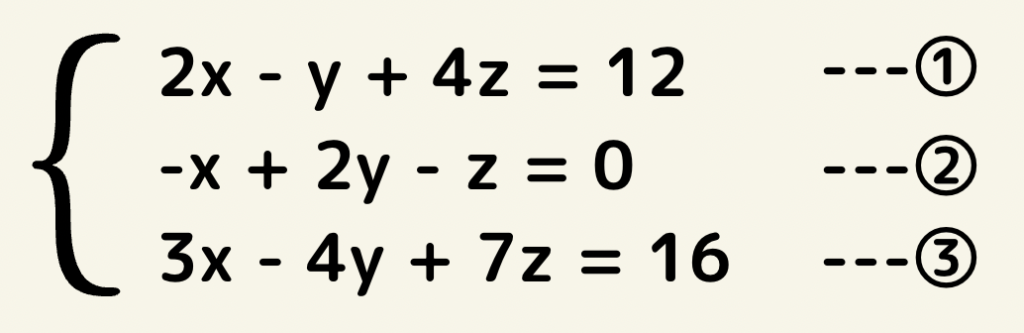
すごくややこしそうですね^^;
ですが、勘のいい方なら気づくはず。
そう、文字を減らせばいいんです。中学生で学んだ連立方程式の解き方、加減法、代入法を使えば解くことができます!
では実際解いてみましょう!
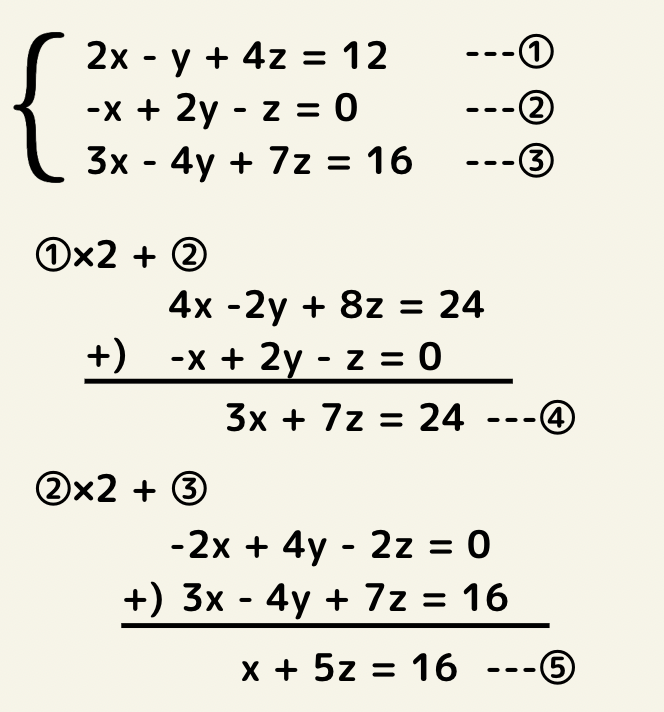
まずは文字を消去しないといけませんが、一度に減らせるのは基本的には1つです。
今回はyを減らしてxとzの2元1次方程式を2つ作りましょう!
まず①と②の式から④の式を作り、同様に②と③の式から⑤の式を作ります。
ここまで来れば後は今までと同じです!
④と⑤の式で2元1次連立方程式が作れます!

このようにxとzを求めることが出来ます。
最後に求めたx=1,z=3を元の式のいずれかに代入すればyの値が求まります。
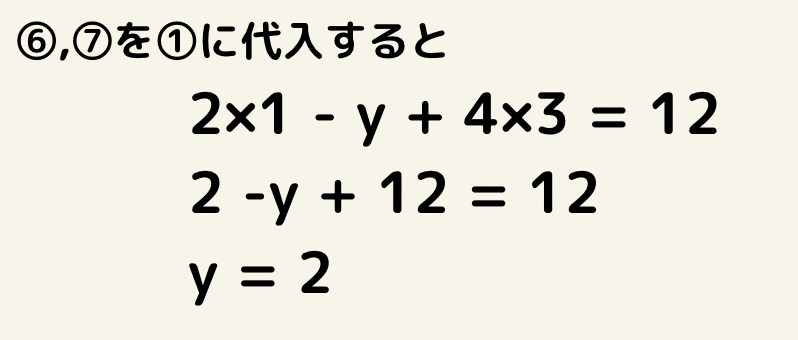
よって答えは(x,y,z)=(1,2,3)となる。
3元1次の連立方定式の解法手順
①消去する文字を決める
②消去する文字が消えるように加減法を用いて文字を消去
③同様に別パターンの式の組み合わせで決めた文字を削除
④出来た2つの式で連立方程式をたてる。
⑤2つの文字の値を初めの3つの式どれかに代入をして求める。
こうやって解いているといかに中学の数学が高校数学にとって大切かがわかりますね^^
これで連立方程式もバッチリですね!
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
京の算数学 解答#186
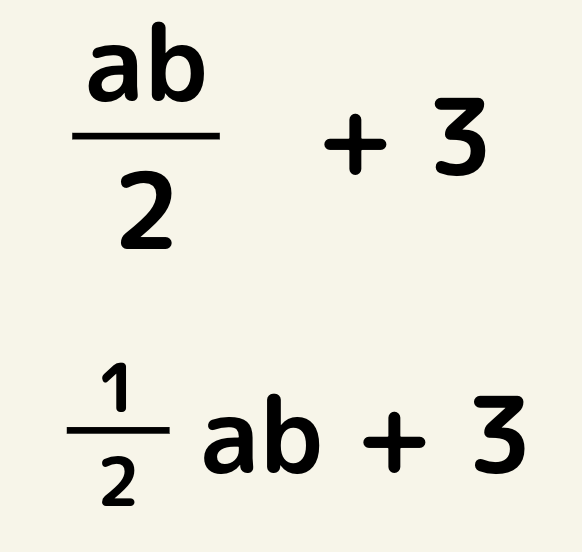
どちらでも正解です!
文字式のルールは
・×と÷は省略すること
・1つの項において数字、アルファベット順にする。例:y × x × 2=2xyにする
と学校では指導される事が多い。


