アイデア数理塾 京の算数学問題#620
算数学コラム
みなさんこんにちは！京都市中京区で塾を運営しております。油谷拓哉（ゆたに たくや）です！
現在新中学1年生は予習を進めています。
その中で捉えづらいのが初めて学ぶ正負の数という概念の広がりです。
特に数字においては大小関係は大事なところ。
今日は正負の数の大小関係についてまとめていきます。
正負の数による概念の広がり
算数から数学になると概念的な広がりが大きくなります。
今まではプラスしかない世界で学んできました。
ですから「3-5は？」と聞かれたら「引けない」というのが正解です。
中学からはマイナスの領域も学ぶので「3-5は？」と聞かれると「-2」となります。
中学数学はいかに今までの思い込みを捨てるのか？ということになります。
０には符号がつかない！？
数字の大小には数直線が非常に便利です。
数直線とは０（原点）を基準とし一方向を＋とし、逆方向を−とします。
多くの場合は右側をプラスにします。
ここで出てくる疑問の１つが０は「＋なの？―なの？」です。
０は原点といいます。
つまり＋かーの真ん中を意味するので＋も−もつかないのです。
正の数の大小関係を学ぼう
正の数の大小はシンプルです。
数字が大きい方が大きいのです。
つまり数直線の右を正とするなら、右に行けば行くほど大きくなります。
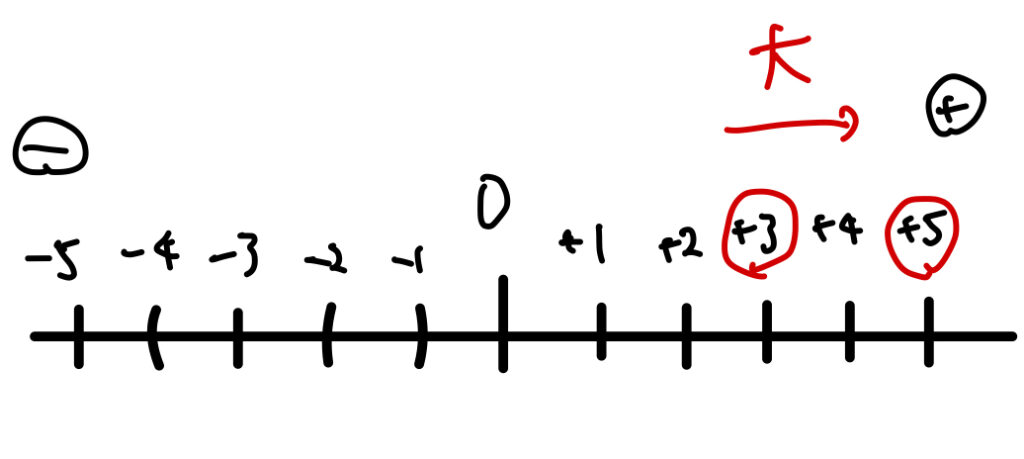
+3と+5であれば+5の方が大きくなります。
ただここで難しいのは小数と分数です。
大小関係を理解するためにはまずは分数を小数に直せるようにしておきましょう。
負の数の大小関係のコツ
負の大小関係は注意が必要です。
数直線で右を正にするとしたら左は負になります。
つまり左に行けば行くほど小さい数になります。
言い換えると右に行けば行くほど大きくなるといえますので、数直線の覚え方は右側にある数字が大きいと覚えておきましょう！
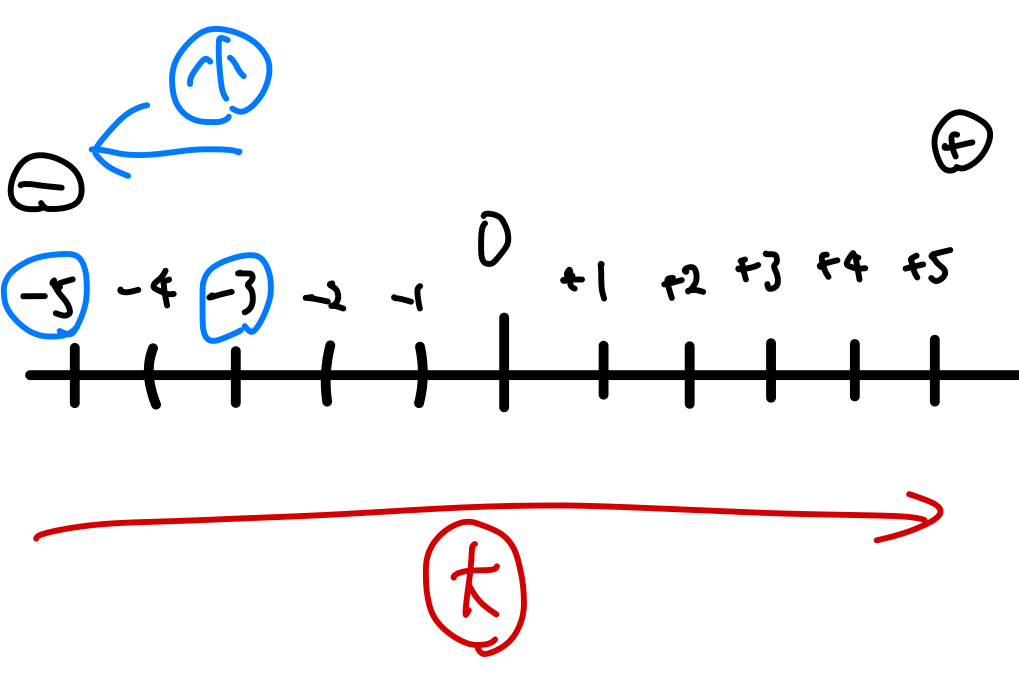
-5と-3であれば-5の方が左側にあるので小さくなります。
つまり大小関係を理解するためのはこの数直線がイメージできるかどうか？が鍵になるのです。
正負の数は丁寧に繰り返そう
正負の数は中学数学の入り口です。
この単元や解釈を理解せずに先へ進んでしまうと十中八九、数学の点数は安定しません。
今のうちに予習をするメリットは時間をかけて入り口を丁寧に繰り返そうという意味なのです。
以上！京都市中京区のアイデア数理塾 油谷拓哉（ゆたに たくや）がお届けいたしました！
算数好きあつまれ〜！
京の算数学 解答#620
