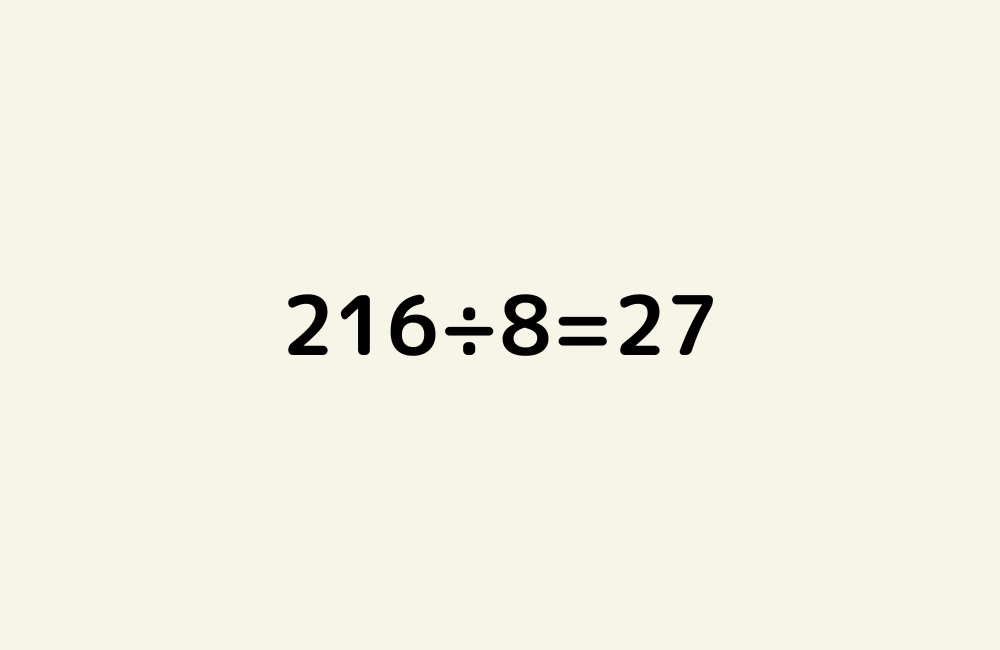数学コラムの目次
- 1 京の算数学問題#1315
- 2 アイデア数理塾はこちら
- 3 算数学コラム
- 4 京の算数学 解答#1315
- 5 おすすめの算数学ブログ
京の算数学問題#1315

アイデア数理塾はこちら
算数学コラム
「割合だけ、どうしても分からない…」
でも実は、割合そのものが難しいというより、
ほとんどが
- 分数(=“○/○”の感覚)
- わり算の意味(“1あたり”“何倍”)
- 単位量あたり(=1あたりにそろえる)
この3つが身についていない可能性が高いんです。
小学校の学習内容的にも、単位量あたり→割合は一連の流れとして扱われます。
だから復習は「割合のプリントを解きまくる」より、原因の階段を1段ずつ戻るのが遅いようで1番早いです。
まず確認してみよう!:割合が苦手な子の“つまずきパターン”3つ
パターンA:式は立つけど、どっちで割るか毎回迷う
→ もとにする量の感覚が弱い(単位量あたりの問題 “何を1と見るか”が曖昧)
パターンB:文章題になると止まる
→ 「くらべる量」「もとにする量」が文から拾えてない(読解力の問題)
パターンC:分数・小数・百分率が混ざると崩れる
→ 分数の同値(同じ大きさ)や、小数⇄分数⇄%の変換が弱い
復習の結論:この順で“戻る”と最短で直ります
割合は、ざっくり言うと
割合 = くらべる量 ÷ もとにする量
=「何倍?」
=分数で言えば「くらべる量 / もとにする量」
この感覚を作るために、復習はこの順番がベストです。
- 分数(同じ大きさ・分ける)
- わり算の意味(1あたり/何倍)
- 単位量あたり(1あたりにそろえる)
- 割合(もとを1と見る)
- 百分率・割引(100を基準にする)
※「単位量あたり」「割合」は小5でまとまって出ることが多いので、戻り学習もしやすいです。
STEP1:分数まで戻る(ここが弱いと割合は必ず崩れる)
①「1/2」「1/4」など“等分”がイメージできる?
チェック問題(口でOK)
- ケーキを4人で同じに分けたら、1人分は? → 1/4
- 1/4が3つ分は? → 3/4
ここがあやしい子は、“分数=分けた数”の感覚が身に付いていません。まずは絵(円・テープ)でOK。
② 同じ大きさの分数(同値分数)が言える?
- 1/2 = 2/4 = 3/6
ここの解釈が弱いと、「割合=分数」になった瞬間に迷子になります。
③「〜の何分の何」タイプができる?
例:12の 2/3 は?
計算:12 × 2 ÷ 3 = 8(12 ÷ 3=4、4×2=8)
コツ:先に割れるなら割ってから掛ける(計算もラク・ミスも減る)
STEP2:わり算の意味を整理する(“計算”じゃなく“意味”)
わり算は大きく2種類あります。
- 等分除(とうぶんじょ):同じ数ずつ分ける
例:12個を3人で分ける → 1人4個 - 包分除(ほうぶんじょ):何個分あるか(何倍・何回分)
例:12個を4個ずつにすると何組? → 3組
「何倍か」をわり算で出す練習が大切
例:
Aは6cm、Bは3cm。AはBの何倍?
→ 6 ÷ 3 = 2倍
この「何倍?」がそのまま割合に繋がります。
STEP3:単位量あたり(=1あたり)を“毎回1にそろえる”
割合が苦手な子に、いきなり「もとにする量」と言っても難しいです。
だから先に 単位量あたり(1あたり)を固めると一気に楽になります。
単位量あたりの基本
- 600円でりんご3個 → 1個あたり?
600 ÷ 3 = 200円/個 - 2Lで4日 → 1日あたり?
2 ÷ 4 = 0.5L/日
ここで「÷する相手が“1にするための数”」って感覚が育つと、割合の式が自然になります。
STEP4:割合に戻る(“もと”を1と見るだけ)
割合の公式はこれだけ。
割合=くらべる量 ÷ もとにする量
まずは図で「どれが“もと”?」を決める
おすすめはテープ図(棒の図)です。
- もと(全体)=100だと思って棒を1本描く
- くらべる量(部分)=その中の何割・何%か
超基本問題でパターンを身につける
例:
定員50人のクラスに40人います。割合は?
→ 40 ÷ 50 = 0.8 = 8割(80%)
※0.8=80%(×100)
※8割=80%(割→%)
STEP5:百分率・割引は「100をもとにする」だけ
割引が苦手な子は、ここで混乱します。
- 20%引き=もとの0.8倍
- 30%増し=もとの1.3倍
例:2000円の20%引き
2000 × 0.8 = 1600円
先に「何倍?」に直すと比較的ミスが減ります。
家庭学習のやり方:1日15分×10日で立て直すプラン
Day1-3:分数(絵+同値+〜の2/3)
- 1/2=2/4 の言い換え
- 12の2/3、15の3/5 みたいな“割って掛ける”練習
Day4-6:わり算の意味+単位量あたり
- 600円で3個 → 200円/個
- 300mを6秒 → 50m/秒 みたいに「1あたり」
Day7-10:割合→%→割引
- くらべる量÷もと、の型固定
- 0.25=25%=2.5割 みたいに変換
ポイント:毎日「同じ型」を繰り返す。問題数より“型”の定着が勝ち。
あるあるなミスと、直し方
ミス1:割る数が逆になる
→ もとにする量=“基準”を先に丸で囲む
(「全体」「定価」「もともと」などの言葉を探す)
ミス2:%が出ると急に怖くなる
→ まずは 小数のまま答えを出してOK
最後に×100するだけ、に分ける
ミス3:文章題で迷子
→ いきなり式を書かずに、先にこれだけ書く
- もと:
- くらべる:
- 求める:割合(=÷)
つまずきが深刻なときは「教わり方」を変えるのが近道
割合は“積み上げ”なので、どこが穴かを見つけて埋めるのが重要です。
京都市の中京区あたりで、算数(割合・分数)のつまずきを単元から戻って整理したい場合は、ぜひ当塾におまかせください!
アイデア数理塾では「分数→単位量あたり→割合」まで戻って整える方針などその生徒に合わせた学習プランを立てて、復習を行なっていきます。
京の算数学 解答#1315