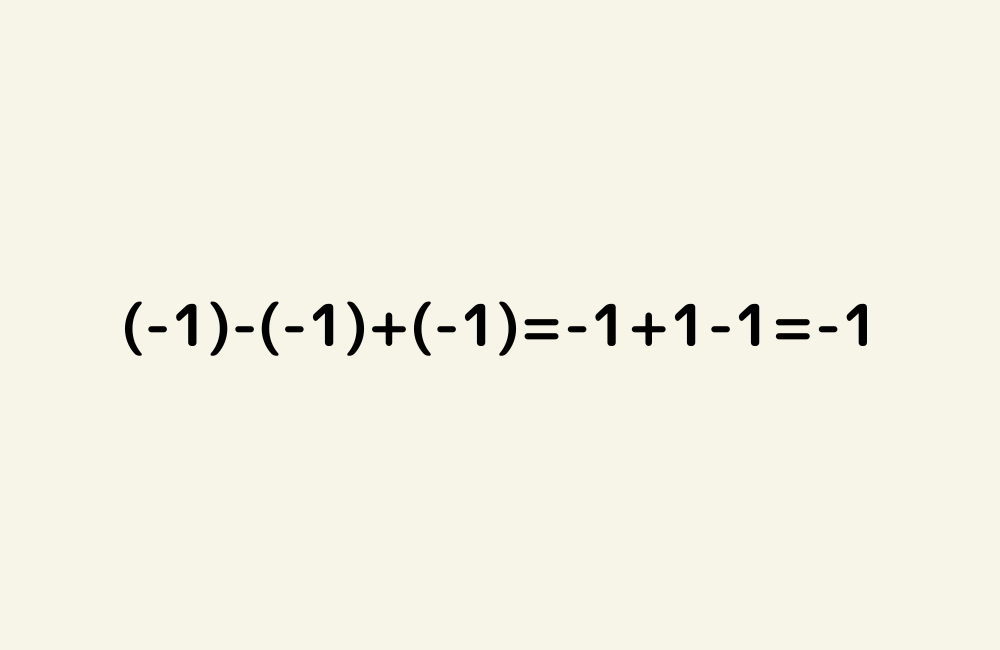数学コラムの目次
京の算数学問題#996

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で学習塾を運営しております、油谷拓哉(ゆたに たくや)です。
新中学1年生のみなさん、中学数学の予習は順調に進んでいますか?
中学に入ると、算数から数学へと学びが大きく広がります。その中でも最初に出てくるのが「正負の数」です。
この正負の数は、小学校で学んだ「数」の概念を大きく広げる重要な単元ですが、最初は戸惑う生徒が多いです。
今日は、この「正負の数」の大小関係について、分かりやすく解説していきます!
正負の数による概念の広がり
算数から数学に進むと、「数」の概念が広がります。
小学校までは「正の数」だけ
これまで小学校で扱ってきたのは、基本的に正の数だけでした。
たとえば…
3 – 5 = ?
小学校では「引けないからできない」と教わってきましたよね。
中学から「負の数」が登場
中学では「負の数」が登場します。
3 – 5 = -2
「負の数」という新しい概念を理解することで、今まで「引けない」と思っていた計算が可能になるのです。
数学は「これまでの常識」を広げていくことから始まります。
数直線で正負の関係を理解しよう
正負の数の大小関係を理解するには、数直線をイメージすることが重要です。
数直線の基本ルール
- 0(ゼロ)を中心にして、
- 右側 → 正の数(+)
- 左側 → 負の数(-)
数直線上で、右側にある数が大きいというルールを覚えておきましょう!
0には符号がつかない!?
ここで「0」の扱いについて疑問が出てきます。
0は+でも-でもない
- 0は「正」とも「負」とも言えません。
- つまり「0は中立的な存在」=「原点」なのです。
0を基準にして、
- 右に進むと正の数
- 左に進むと負の数
と覚えると、正負の数の位置関係が理解しやすくなります。
正の数の大小関係
正の数はシンプルです。
数が大きいほど大きいと考えればOKです。
+3と+5なら→ +5の方が大きい
小数や分数が入るとどうなる?
小数や分数も正負の数に含まれます。
正の数どうしの大小を比べるときは、
分数を小数に直してから比べると分かりやすくなります。
たとえば、
3/4=0.75と0.8
→ 0.75 < 0.8 だから、0.8の方が大きい
負の数の大小関係
負の数の大小関係は、正の数とは逆になります。
数直線で考える
- 右に行くほど大きくなる
- 左に行くほど小さくなる
-3と-5を比べると
- 数直線では-3が右側にあるので-3の方が大きい
つまり、負の数は絶対値(プラスに直した値)が大きいほど、小さくなるという感覚が重要です。
正負の数の大小関係 まとめ
正の数同士 → 数が大きい方が大きい
負の数同士 → 数直線で右にある方が大きい
正と負 → 正の方が常に大きい
0 → 正でも負でもない中立的な存在
正負の数をしっかり理解するコツ
① 数直線をイメージする
- 数直線を「右に行くほど大きい」と覚える
- 「0」を中心にした左右の関係を意識する
② 分数や小数を変換する
- 大小を比べるときは、小数や分数をそろえてから考える
③ 何度も繰り返して定着させる
- 正負の数は中学数学の入り口
- ここでつまずくと、今後の計算が難しくなる
予習をするメリット
中学数学が始まる前に「正負の数」を理解しておくことで、
- 学校の授業がスムーズに理解できる
- 計算問題でつまずきにくくなる
- 数学の苦手意識が減る
最初が肝心!
今のうちにしっかり正負の数を身につけておきましょう!
まとめ
正負の数は中学数学の基礎になる大切な単元です。
- 数直線を使ってイメージする
- 正負の関係をしっかり理解する
- 小数や分数を含めて大小関係を確認する
最初は戸惑うかもしれませんが、しっかり反復して慣れていけば必ずできるようになります!
以上、京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けしました!
算数好きあつまれ~!
京の算数学 解答#996