数学コラムの目次
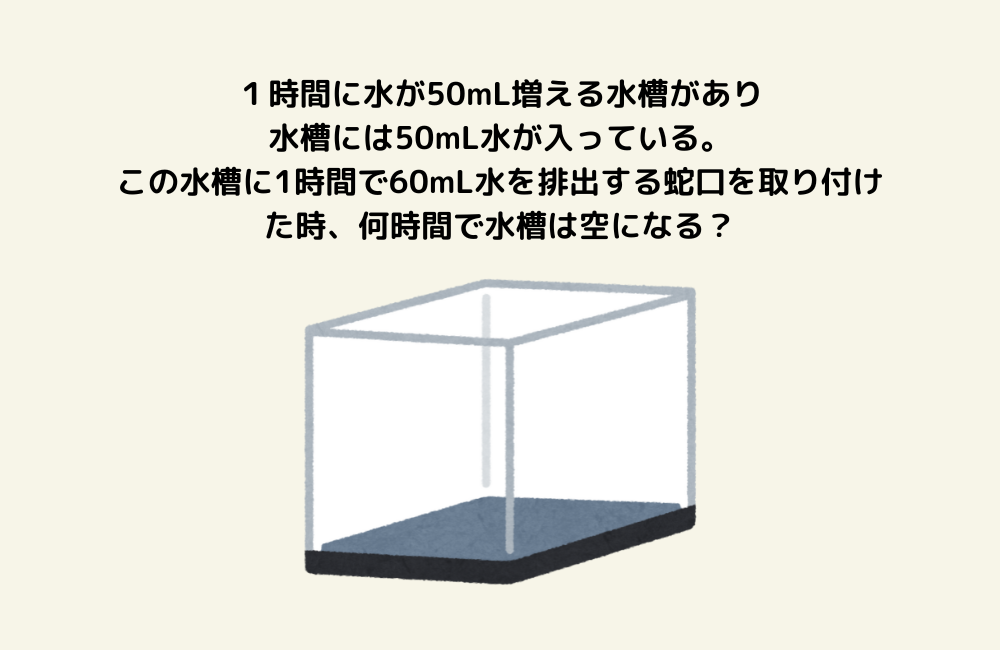
京の算数学問題#819
アイデア数理塾はこちら
算数学コラム
「1+1=2」を証明せよ。
こう聞かれて、あなたはどう感じるでしょうか?
「そんなの簡単!」と思うか、
「え?どういう意味?」と考えてみるか。
実は、この問題、大学の数学科でも解けない人が続出するレベルの難問なんです。
ちなみに、僕も途中で挫折しました(笑)。でも、実際にこの話はとても面白い。私たちは普段、1+1=2を当然のこととして使っていますが、そこには深い数学の美しさが隠されています。
まず、最初に立ち返るべきなのは、「数とは何か?」という問いです。
「1」とは何か?
「2」とは何か?
「+」や「=」という記号の意味は?
これらの基本的な概念に立ち戻らなければ、「1+1=2」の証明は始まりません。
1+1=2は仮定
「1+1=2」とは、実は証明された事実ではなく、数学の中での仮定として成り立っています。
この段階で、数学嫌いな方は「もうやめてくれ」と思うかもしれませんね(笑)。私も同じ気持ちでした。
以前、1+1=2の証明に100ページ以上を費やしたという話を聞いたことがあります。これ、本当です(笑)。
数学基礎論や集合論といった分野は、まさに「研究レベル」の内容です。そう考えると、「1+1=2が常に正しいか?」という問いも、あながち簡単には答えられません。たとえば、2進法では1+1=10となりますし、他の進法ではまた異なる結果になることもあります。
別の視点から考える
「1+1=2」という基本的な事実も、異なる視点から見ると、また新たな洞察が得られます。
数学の面白さは、こうした別の切り口からアプローチできるところにあります。
簡単に見えるものほど、実は難しい。そして、当たり前のことほど、疑ってみる価値があるのです。
私が1+1=2の証明を通じて感じたのは、まさにこの部分です。
自分が簡単にできていると思っていることでも、いざ人に伝えようとすると難しかったり、うまくいかないときは当たり前にやっていたことを深掘りする必要があるということです。そうすると、新しい気づきが得られます。
数学の思想と生き方のヒント
私が運営している「アイデア数理塾」の基本的な考えは、ただ数学の定理を使えるようにすることだけではありません。
それよりも、そこからイメージを膨らませて、自分の人生に役立てていくことを目指しています。
例えば、解の公式について話しましょう。
多くの生徒が「x=の公式」を覚えていますが、実際には「ax²+bx+c=0の時」という前提条件があって初めて成り立つ公式です。
このように、すべての定理や公式には「前提条件」があります。
「こういう条件のもとで成り立つ」という前提があるのです。
ビジネスでも同じです。成功者の成功法則をそのまま真似してもうまくいかない理由は、その成功者が成功したタイミングや環境といった「前提条件」が見えていないからです。実は、成功の秘訣はやり方そのものではなく、その人が置かれていたタイミングや環境にあったりするのです。
もし「うまくいかない」と感じた時は、自分が適用している方法の「前提条件」を見直してみましょう。すると、不調の原因が見えてくるかもしれません。
数学とは、まさに哲学のようなものです。そして、私が日々接している生徒たちは、私よりも柔軟な発想を持っています。彼らの考え方からも多くを学ばせてもらっています。
以上、京都市中京区の「アイデア数理塾」油谷がお届けしました!
京の算数学 解答#819




