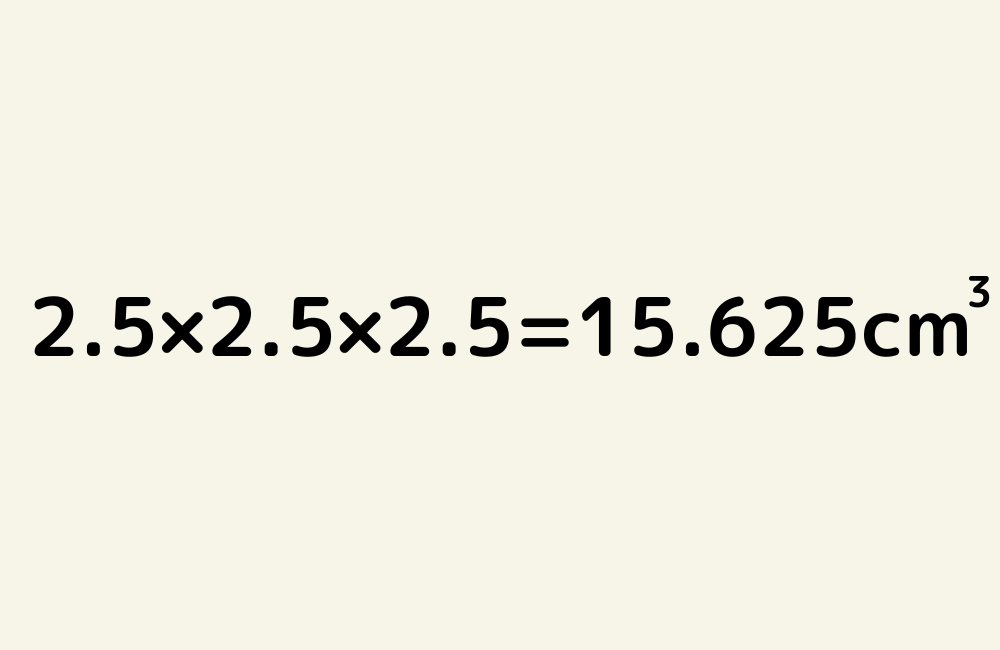数学コラムの目次
京の算数学問題#726

アイデア数理塾はこちら
算数学コラム
みなさんこんにちは!京都市中京区で塾を運営しております。油谷拓哉(ゆたに たくや)です!
たて×横×高さで求められる体積。面積と比べて日常生活で求める機会は少ないかもしれませんが、算数や数学の問題ではたくさん出てきます。小学5年生の算数科の学習で初めて登場しますが、子どもたちにとって、立体物は具体的に想像しにくいもの。つまずいてしまう子も少なくありません。今日のブログは体積と容積についてです。
体積の意味「何を基準に考えるか?」
体積に限らず算数で大切になってくるのは、「何をもとにして考えるか」ということです。
たて2cm、横3cm、高さ4cmの直方体とたて2cm、横2cm、高さ5cmの直方体では、どちらの体積が大きいでしょう。
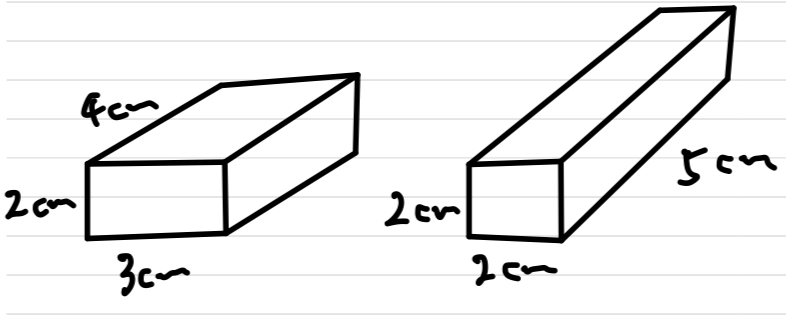
この2つが実際にあったとしても直接比較することはできません。
だからもとにする大きさを決めて、そのいくつ分かを考えます。
この場合は、1cm×1cm×1cm=1㎤(1立方センチメートル)をもとにして考えます。1㎤がいくつ分かで体積を表すということです。
公式として「体積=たて×横×高さ」と覚えても答えは求められるのですが、それがなぜなのかを説明できるとより深い理解につながります。
体積と容積の違いとは?
ここまで理解できていても、難しく感じるのが容積の問題です。
容器の厚さを考慮し、実際に容器に入る分の体積を求めます。
箱の厚み(内のり)が1cmの場合で考えたいと思います。この問題では3つのステップでつまずくことがあります。
①そもそも容積の概念が理解できない
②内のりの部分を引く想像ができない
③②まではわかるが、底面の部分の想像ができない
①は具体物を使い、1㎤のブロックを並べたり、水を入れて水が入る部分だけを求めるということを伝えるとイメージできるようになります。具体物でよく用いるのは、私の場合は升(ます)です。升の場合は木のつなぎめがわかりやすいので、内のりもイメージしやすくなります。
②は①を使い、実際に容器に入っている部分の長さを測ると分かります。ただし、内のりが1cmの場合、外側の辺の長さから両側の2cm分を引くことになります。問題文の数字としては1cmですが、辺の長さを求めるには2cmずつ引かなくてはならないということです。
なぜ2cm内のりの2つ分を引かないといけないのか?が理解できれば容積の理解はもう少しです。
③は②まで理解できているので、機械的に3辺とも2cmずつ引いてしまいそうになります。ですが、高さは、底面の1cm分のみを引くことになります。底の内のりだけを引くというのがポイントです。
最近では100円ショップでも升が売られていたりします。もし容積でつまづいていたらお試しください。
今回は、体積や容積を例に考えました。算数ではこのように、一問一答的なやり方ではすぐに答えにたどり着けず、答えを求めるための材料集めからしなくてはならないことがあります。そこが難しさであり、楽しさでもあります。公式を覚えて使いこなす力も必要ですが、たまには基礎基本に立ち返って考えてみてはいかがでしょうか。
以上!京都市中京区のアイデア数理塾 油谷拓哉(ゆたに たくや)がお届けいたしました!
算数好きあつまれ〜!
京の算数学 解答#726