数学コラムの目次
京の数学学問題#218

アイデア数理塾はこちら
算数学コラム
今日は中学生で学ぶ因数分解のやり方をわかりやすく解説していきます。
因数分解は中学3年生のちょうど夏休み前後の時期に学ぶことが多い単元です。
この単元は得点源になる範囲ですのでしっかりと予習復習をしておきましょう!
因数分解とは?
因数分解とは和と差の式を積の式に変換する事を言います。
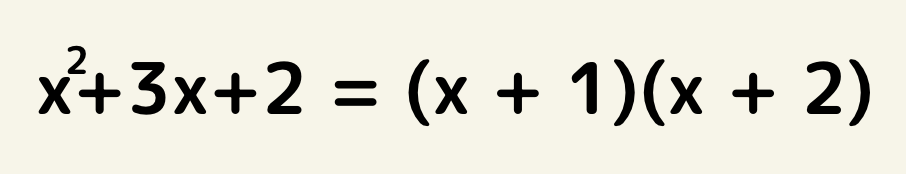
上記の式であれば、左辺が和と差の式、右辺が積の式になります。
因数分解は概念も含めて計算をする際に非常に重要な範囲ですので展開と合わせて覚えておくようにしましょう。
因数と素数
因数とは
1つの式や数を分解して積の形にした時の各要素の事を言います。
例えば、30=5×6
この場合は5と6を因数と言います。
それを文字で表すと

この場合
因数はaと(x+y)になります。
特に左辺のaはax,ayどちらにも含まれているので共通因数と言います。
素数とは
2以上の自然数で正の約数が1と自分自身のみである数字のことです。
例えば、13は1と13しか約数はありませんので素数となります。
4は1,2,4が約数なので素数ではありません。
素数の研究は進められていて、現時点で2を8258万9933回かけた数から1を引いた数が判明している最大の素数と言われています。
また、よくある問題として「1」は素数なのか?というのがあります。
定義にあるように2以上を素数とするので1は素数ではありません。
【問題】
次の数字の中から素数を選びましょう!
1,11,42,51,73
【答え】
11,73
素因数分解とは?
素因数分解とは、ある数を素数のかけ算で表すことです。
因数はかけ算に表記したものなので、無数に出てきてしまいますよね。
例えば36を分解すると6×6、2×18,3×12など全て因数です。
素因数分解では
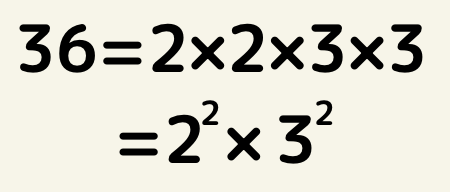
簡単にいえば分解できないところまで徹底的にやりましょう!と覚えてもらえれば良いです。
素因数分解のやり方
108を素因数分解しましょう。
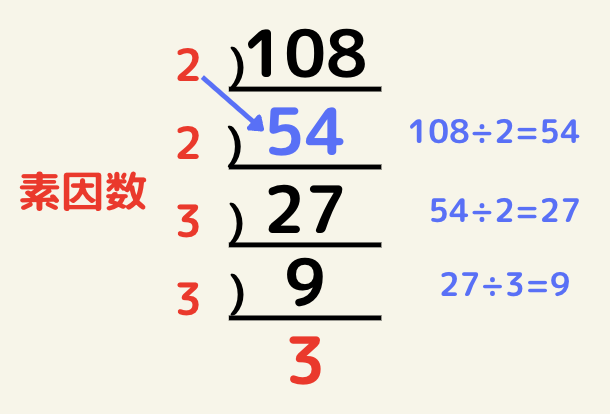
108を順番に素数で割れなくなるまで割っていきます。
この場合だと108=2×2×3×3×3=2^2×3^3
が答えになります。
【素因数分解の便利さがわかる問題】
(1)108にできるだけ小さい自然数nをかけてある自然数の2乗にしたい。
自然数のnを求め、どんな数の2乗になるか?答えよ。
(解答)
108を素因数分解すると108=2×2×3×3×3なので2が2個、3が3個かけられています。2乗にしたい場合は、3をかけると2^2×3^4=(2×3^2)^2となるので、かける自然数n=3、(2×3^2)^2=18^2なので18の2乗になる。
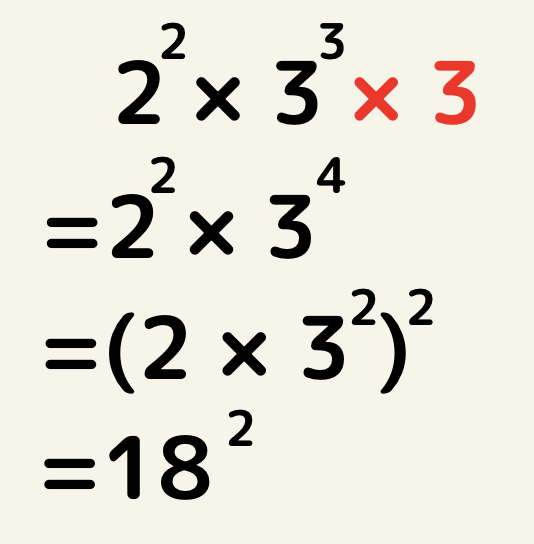
(2)294にできるだけ小さい自然数mで割りある自然数の2乗にしたい。
自然数のmを求め、どんな数の2乗になるか?答えよ。
(解答)
294を素因数分解すると、
294=2×3×7×7=2×3×7^2
つまり、2×3=6で割ると
7^2=49 つまり、自然数m=6、7の2乗になる。
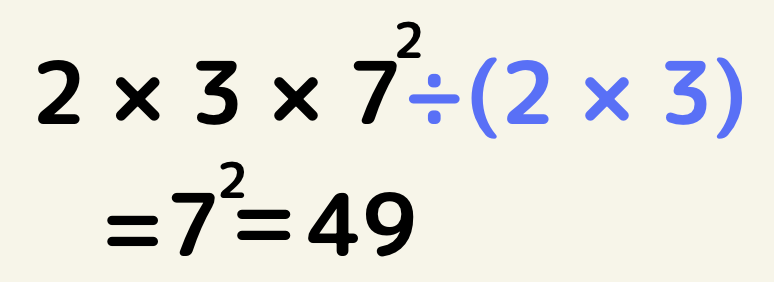
このように素因数分解で数字を表せると何を書けたら2乗になるのか?どう言う構造をしているのかがわかります。
慣れてくると約分も早くなりますよ^^
展開と因数分解

因数分解は展開とセットで覚えておきましょう。
因数分解の意味は「和と差の式を積の式に変換する」でしたね。
展開はこの反対で「積の式を和と差の式に変換する」です。
因数分解と展開はこの後の2次方程式や高校で学ぶ3次方程式でも使います。
この範囲は基礎中の基礎であるのできちんと演習をして理解しておきましょう!
因数分解の公式
展開公式の基礎型
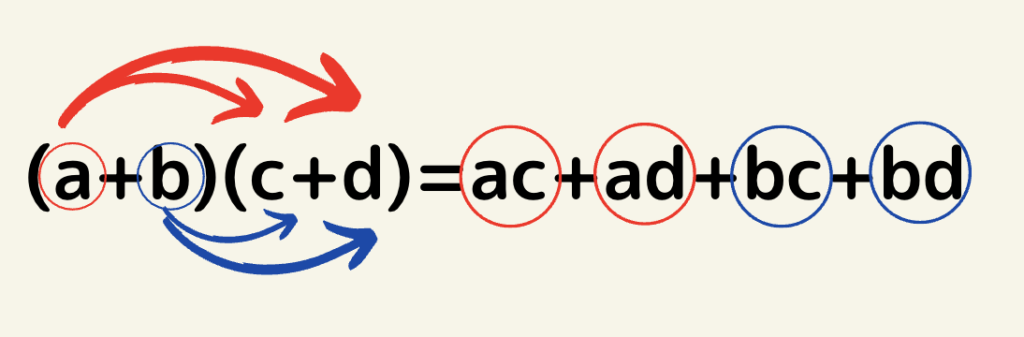
展開公式の基本はこの式です。
(a+b)(c+d)の場合、)(a+b)のaを(c+d)のそれぞれにかけ、bも同様にかけていく。
全ての展開公式のベースがこの式ですので是非とも覚えておきましょう。
例えば、
(x+y)^2=(x+y)(x+y)=x^2 + xy + xy +y^2=x^2 +2xy +y^2と展開公式が出来上がります。
展開・因数分解の公式まとめ

繰り返しになりますが展開と因数分解はセットです!
どの項がどの場所に対応しているのか?を意識しながら因数分解の問題を解いていきましょう。
展開のやり方
【問題】
次の式を展開してみよう。(x^2とはxの2乗という意味です。)
(1)3a(x+3)
(2)(x+3)(x-2)
(3)(x+5)^2
(4)(x-7)^2
(5)(x+3)(x-3)
(6)(x+1)(y-3)
【解答】
(1)3aを順に()内の各項にかけていく。 3ax +9a
(2)公式2よりa×b=-6 a+b=1 なので x^2+x-6
(3)公式3より 2xy=2×5×X=10x 5^2=25だからx^2 + 10x + 25
(4)公式4より 2xy=2×(-7)×X=-14x (-7)^2=49 なので x^2 – 14x + 49
(5)公式5より x^2-(3)^2なのでx^2 – 9
(6)展開の基本公式より x × y + x × (-3)+ 1 × y + 1 x (-3)なのでxy -3x +y -3となる。
展開の問題はもし間違えそうなら展開の基礎公式で全て解答できるので迷ったら基礎公式と覚えておこう!
因数分解のやり方
【問題】
次の式を因数分解してみよう。(x^2とはxの2乗という意味です。)
(1)2ax + 4ay
(2)x^2 +4x -5
(3)x^2+ 6x + 9
(4)x^2 -20x +100
(5)x^2-81
【解答】
(1)共通因数は2aなので、2a(x+2y)
(2)2の因数分解公式よりまずはa×b=-5の組み合わせを探していきます。1×(-5)か-1×5なので、a+b=4になる組み合わせは、-1×5になります。つまり、(x-1)(x+5)
(3)(2)と同様に2の公式で考えていきます。a×b=9の組み合わせは(a,b)=(1,9)(3,3)(9,1)(-1,-9)(-3,-3)(-9,-1)でこの中から、a+b=6のパターンを探すと(a,b)=(3,3)が当てはまります。ですので、(x+3)(x+3)=(x+3)^2となります。これの間の工程を省略したのが因数分解公式3です。
(4)(2)と同様にa×b=100の組み合わせの中でa+b=-20になる組み合わせを考えると、今回は(a,b)=(-10,-10)が該当します。(x-10)(x-10)=(x-10)^2
(5)今回は5の公式を使います。この公式の形は特徴的なので比較的覚えやすいです。
y^2=81の組み合わせは、9×9ですので、(x+9)(x-9)が解答となります。
因数分解を図形で理解しよう
今までの公式は演算で解く事ができますが本質的な部分は面積を用いると比較的わかりやすくなります。
公式を覚えきれていない段階はこのような方法を使えば解答する事ができますので合わせて覚えておくと良いです。
面積での理解にあたり今回も展開と因数分解はセットで理解しておきましょう。
展開公式において
基本公式(a+b)(c+d)=ac+ad+bc+bd
この見方を変えると縦が(a+c)横が(c+d)の四角形の面積であると言い換えれます。
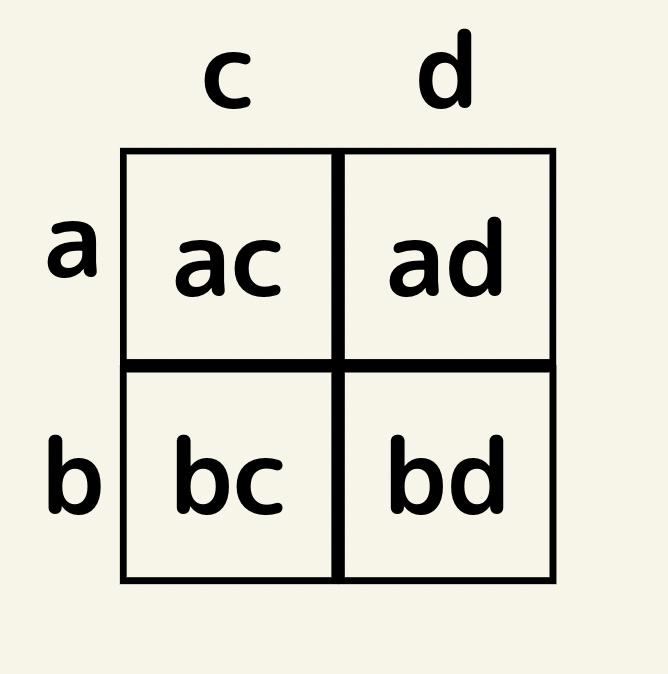
同様に他の公式も
(x+a)(x+b)=x^2+(a+b)x+ab
縦が(x+a)横が(x+b)の四角形を考えると
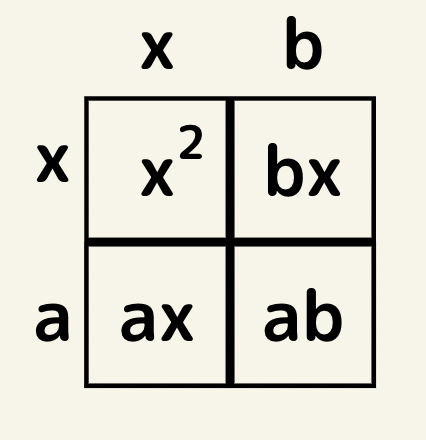
となる。
因数分解の場合
公式1 ax+ay=?
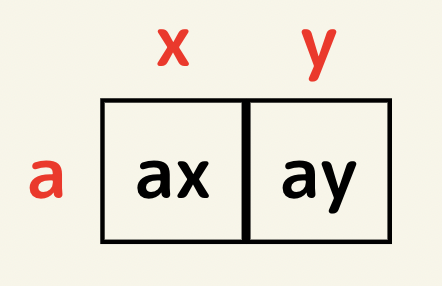
面積がaxになるのは縦がa横がx、面積がayになるには縦がa横がyである必要があるので求める式はa(x+y)となる。
公式2 x^2+(a+b)x+ab=?
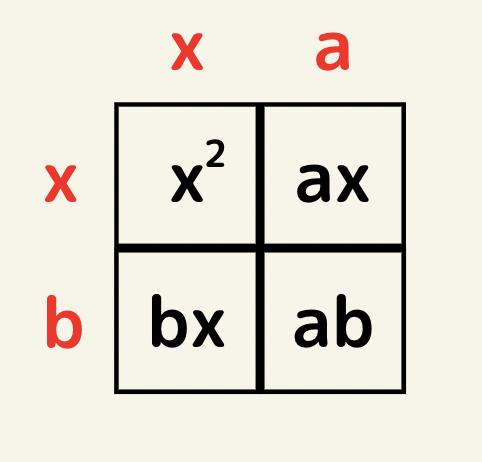
まず考えるのは左上の面積がx^2であるので縦がx横がyとなる。次に右下の面積はabなので、縦がa横がbであり残りの四角も同様に辺の長さが決まる。
よって、(x+a)(x+b)となる。
公式3 x^2+2xy+y^2=?
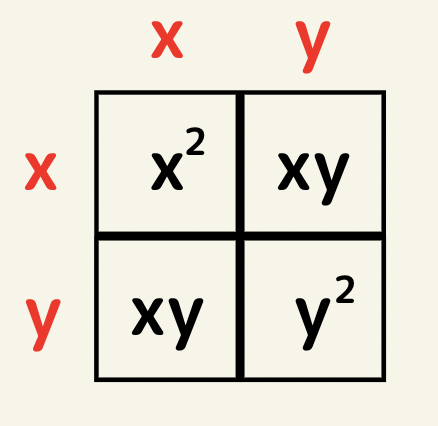
左上の面積がx^2なので縦がx横がxになり、右下の面積がy^2なので縦はy横がyになる。よって(x+y)(x+y)=(x+y)^2
公式4 x^2-2xy+y^2=?
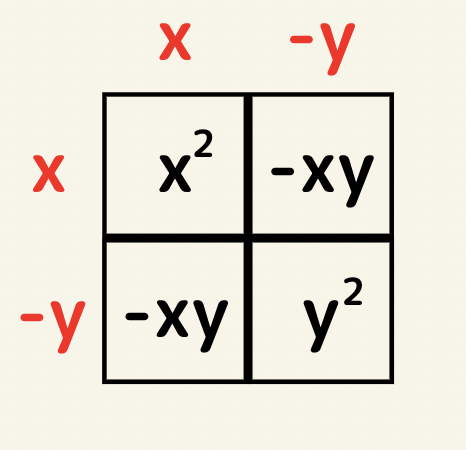
左上の面積がx^2なので縦がx横がxになり、右下の面積がy^2なので縦はy横がyもしくは縦と横が-yになる。ここで、左下と右上の面積が-xyなので縦横は-yと確定できる。よって(x-y)(x-y)=(x-y)^2になる。
※マイナスの場合はこの面積図は違和感があると思うが同様に公式を導けるので気にせず活用しよう。
公式5 x^2-y^2=?
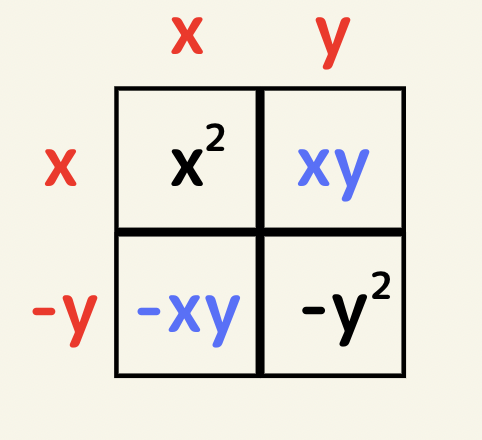
右上の面積はx^2なので縦がx横がxになる。右下の面積は-y^2なので縦、横が-yとyになる。この場合右上と左下の面積は互いに相殺され0となるので、x^2+xy-xy-y^2=x^2-y^2となる。
このように因数分解は公式を覚えてしまえば早いのだが慣れていないうちは図のように面積図を書いて解いてみると間違えずに済む。
因数分解 たすきがけのやり方
【例題と解説】
次の式を因数分解しよう

これを今までの公式で解こうとしても難しいですよね。
こんな場合にはたすきがけと言うテクニックを使います。
たすきがけとは?
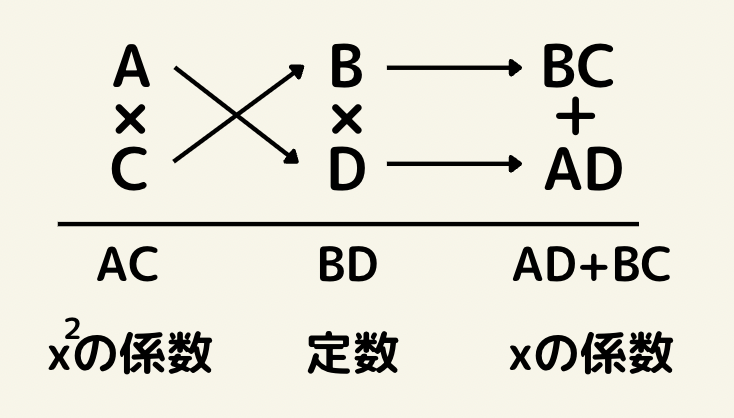
x^2の係数と定数項の因数の組み合わせパターンを考えその中でかけ合わせてBCとADを作りBC+AD=xの係数になるパターンを考えていきます。
例題の場合で考えると
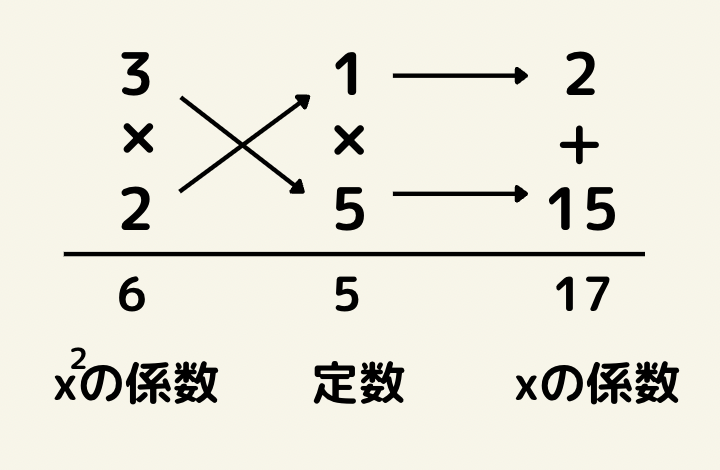
このようになります。
x^2の係数は6なので2×3か1×6の組み合わせです。
定数項は1×5の組み合わせのみです。
xの係数は17ですので、BC+ADの組み合わせは、(3×5)+(2×1)=17なので、答えは(3x+1)(2x+5)となります。
もし答えのイメージがしづらければ、このように書いてみましょう!
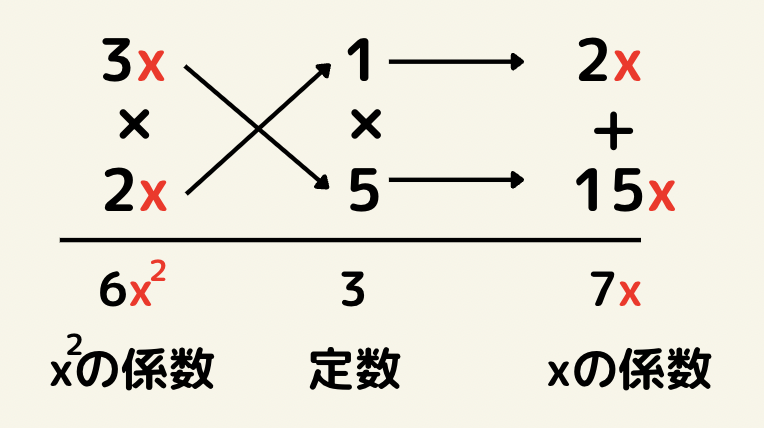
文字で書くと伝わりづらい部分もありますが実際解いてみると慣れてくるのでぜひ一度解いてみましょう!
たすきがけに関してはテクニックというよりも演習量で慣れるのが実は一番王道だったりします。
【問題】
次の式を因数分解しよう!
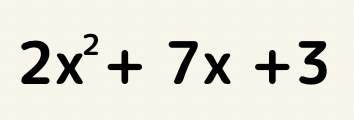
【解答】
たすきがけを用いると
x^2の係数は2だから1×2、定数項は3なので1×3これらを組み合わせて7を作るには、(1×1)+(2×3)=7になる。
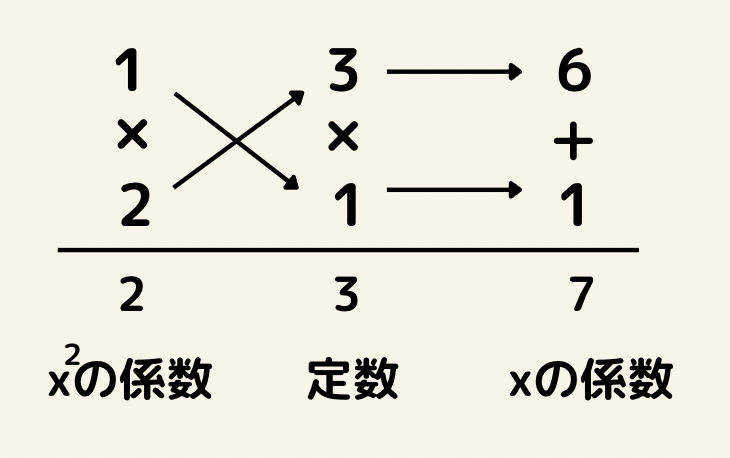
よって、(x+3)(2x+1)になる。
そもそもなぜたすきがけが出来るのか?
例えばax^2+bx+cを因数分解したとしたら。
因数分解した後の形は係数は不明ですが(Ax+B)(Cx+D)の形となるはずですよね。
※係数や項をABCDと仮置きしただけです。
この式を展開した時、ACx^2 + (AD+BC)x + BD となります。
と言う事は、元の式のaにあたるものがACです。
同様にまとめると
a=AC
b=AD+BC
c=BD
となります。
つまりここからたすきがけの決まりが導き出せます。
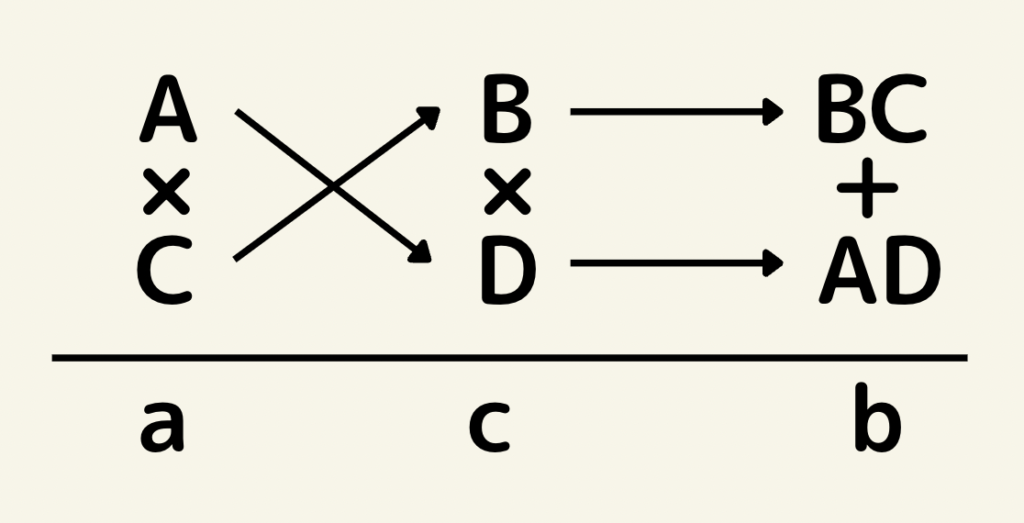
つまり因数分解のたすきがけとは、因数分解が出来たと仮定した時の係数を比較して導き出されたものという事です。
よくある因数分解の特殊解法パターン
置き換えの因数分解
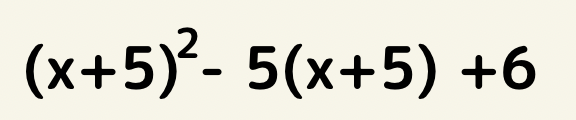
(x+5)=Aと置くと
A^2 -5A +6となります。
因数分解すると(A-2)(A-3)となり、
A=x+5を代入すると
(x+5-2)(x+5-3)=(x+3)(x+2)になる。
この置き換えの因数分解は入試の頻出問題ですのでぜひ押さえておきましょう!
共通因数をくくり出してから行う因数分解
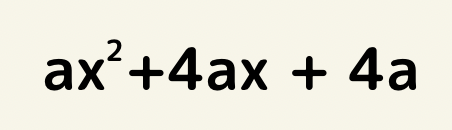
共通因数はaなのでaで括ると
a(x^2 + 4x +4) さらに因数分解すると
a(x+2)^2となる。
一度共通因数をくくりだし、因数分解の公式を使って因数分解をする2回因数分解するパターンの問題です。
1つの文字について整理してから行う因数分解
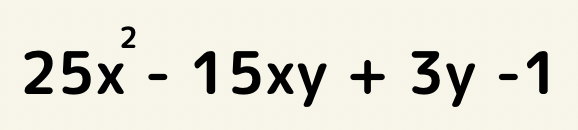
文字の次数を比較し一番次数の低い文字について整理する。
今回はyについて整理をする。(yだけを文字ととらえる)
-3(5x-1)y+25x^2-1
=-3(5x-1)y+(5x+1)(5x-1)
ここでA=5x-1とすると、
=-3Ay+A(5x+1)
=A(-3y+5x+1)
=(5x-1)(5x-3y+1)になる。
対称式の因数分解
対称式とは、x+y=y+xのように文字を入れ替えても答えが変わらない式の事です。
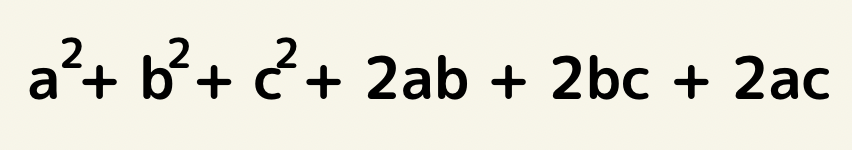
まずは同じ文字(今回はa)について整理をしてみましょう。
a^2 + 2(b+c)a + (b^2 + 2bc + c^2)となります。
a^2 +2(b+c)a + (b+c)^2と因数分解できるので、
置き換える因数分解と同様に、A=b+cとし、置き換えると
a^2 +2Aa + A^2なので
(a+A)^2となり、A=b+cを代入すると
答えは、(a+b+c)^2となる。
交代式の因数分解
交代式とはどの2つの変数を入れ替えても元の式の−1倍になる式の事です。
例えば、x-y=-(y-x)となる式の事です。
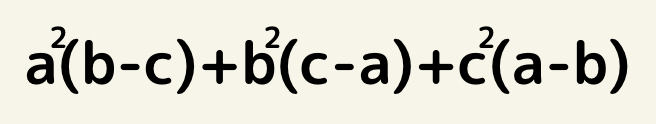
この場合も同様にaについて解いていきましょう
(b-c)a^2 + cb^2 – ab^2 + ac^2 – bc^2
=(b-c)a^2 +(c^2 – b^2)a + cb^2 – bc^2
=(b-c)a^2 – (b+c)(b-c)a + bc(b-c)
ここでA=b-cと置くと
Aa^2 – A(b+c)a + Abcで共通因数Aをくくり出すと
A{a^2 – (b+c)a + bc}
=A(a-b)(a-c)
=(b-c)(a-b)(a-c)となる。
このように因数分解の応用パターンも5パターンしかない事がわかります。
特に中学、高校受験では初めの2パターンを定着させるだけで十分ですのでぜひこの機会にマスターしておきましょう!
因数分解の利用
次の計算を因数分解を利用して解いてみよう!
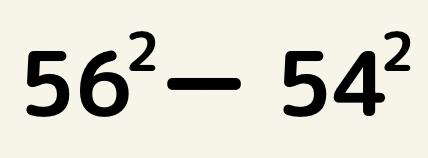
因数分解の公式5
x^2-y^2=(x+y)(x-y)を用いると
(56+54)(56-54)=110×2=220
のように簡単に計算できる。
展開公式の利用パターン問題も覚えておこう!
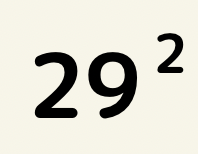
29=30-1と書き換える事ができるので、
29^2=(30-1)^2
(x-y)^2=x^2 -2xy +y^2を活用すると、
30^2 -2×30×1 + (-1)^2=900-60+1=841となる。
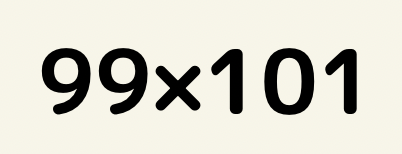
99=100-1
101=100+1 と書き換える事ができる。
(x+y)(x-y)=x^2-y^2の公式を活用すると、
(100-1)(100+1)=100^2-1^2=10000-1=9999となる。
因数分解を使った証明問題
【問題1】
連続する奇数の積に1を加えた数は、4の倍数になる事を証明しよう!
【解答1】
整数nとすると連続する2つの整数は2n+1,2n+3となる。
この積に1を加えた数は、
(2n+1)(2n+3)+1=4n^2 +6n+2n+3+1=4n^2+8n+4=4(n^2+2n+1)
n^2+2n+1は整数なので4の倍数になる。
【問題2】
2桁の自然数の2乗からこの自然数の十の位と一の位を入れ替えてできた自然数の2乗の数を引くとどんな数になるか?
【解答2】
2桁の自然数の十の位をa、一の位をbとすると、元の自然数は10a+bと表せ、各位を入れ替えると10b+aと表す事ができる。
元の2桁の自然数の二乗から桁を入れ替えた自然数の二乗を引くと
(10a+b)^2-(10b+a)^2=100a^2 + 20ab + b^2 -(100b^2 +20ab + a^2)
=99a^2-99b^2=99(a^2-b^2)
a^2-b^2は整数なので99の倍数になる。
【高校】3次式の因数分解
この範囲は数学Ⅰの範囲ですが中学生の因数分解の知識があれば解く事ができます。

特に良く間違えるポイントは-の位置です。
ただ、因数分解の本質は展開の逆でしたよね。
つまり(x+y)^3=(x+y)(x+y)(x+y)という事なのでそれぞれが3回ずつかけられているということになります。ですのでどの項の字数も3になりますよね。
(x-y)^3の場合2項目はx^2 × (-y)なので符号はーになりますし、3項目はx × (-y)^2なので符号は+になります。
公式を忘れた場合は、(x+y)^3=(x+y)(x+y)(x+y)=(x^2+2xy+y^2)(x+y)として導き出しましょう。
何度も言いますがこの範囲はテクニックというよりも数をこなしてパターンにいかに慣れるか?というところになります。
これで因数分解の基本はバッチリですね!
因数分解はこれからの範囲や受験、高校数学でも必須なのでぜひこの機会にマスターしましょう!
以上!京都市中京区のアイデア数理塾 油谷がお届けいたしました!
京の算数学 解答#218




