今日の問題　#019

今日の問題#019

今日のコラム

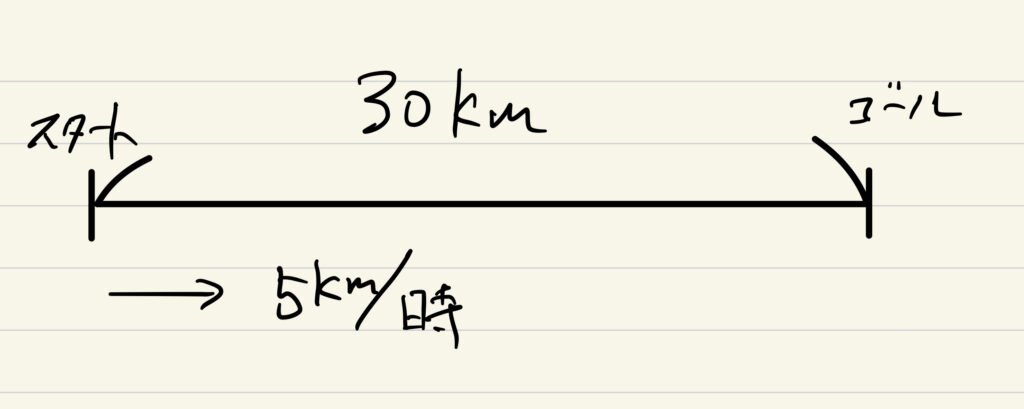
小学校6年生になったら習う速さの問題。

5年生の割合に次いで苦手が勃発するのがこの単元です^^;

今日は中学校に入っても使える単位のお話

早速行ってみよう！

時速1kmとは1時間ごとに1km進みますよという意味です。

これを画像のように表記するのですが、この単位には意味があります。

というか公式覚えなくても単位さえしっかり理解してれば問題は解けます^^

この/を横にぐにゅーんと回転させるとkm÷時間という図式が現れます。

そう！単位は式の意味を教えてくれます。

中学校に行くと文字式というのを習いますので、こういう解釈もできちゃいます。

今日の問題にもあるように時間を求めるためには距離を速さで割る必要があります。

これを単位だけで見ると、kmが消えて時間が残る。

数字だけでOKではなく、単位の動きをしっかりと追っていくと計算ミスをせずに済みます^^

単位を追っていくメリットはこういう単位変換をする時に非常に役に立ちます。

僕も小学生の時、速さの変換には非常に苦労しましたが、この考え方を身につけたおかげで理解することが出来ました。

例えば図のように時速1kmを分速1mに変換するとしたら。

こんな感じで一瞬で解けます。

まず1km=1000mで1時間は60分ですよね。

つまり図のように解釈ができます。

今回は時速1kmから分速1mへの変換でしたがこの解法をマスターすれば逆パターンもできますし、時速5kmになったとしても5をかけたらいいだけなので簡単に計算ができます。

単位変換は分数を多用しますので約分を駆使してできるだけ数字を小さくして計算したいですね。

---

この/を使った単位で思い浮かんだ方もいらっしゃるかもしれませんが、、、

%これはどういう解釈をしたら良いのでしょうか？

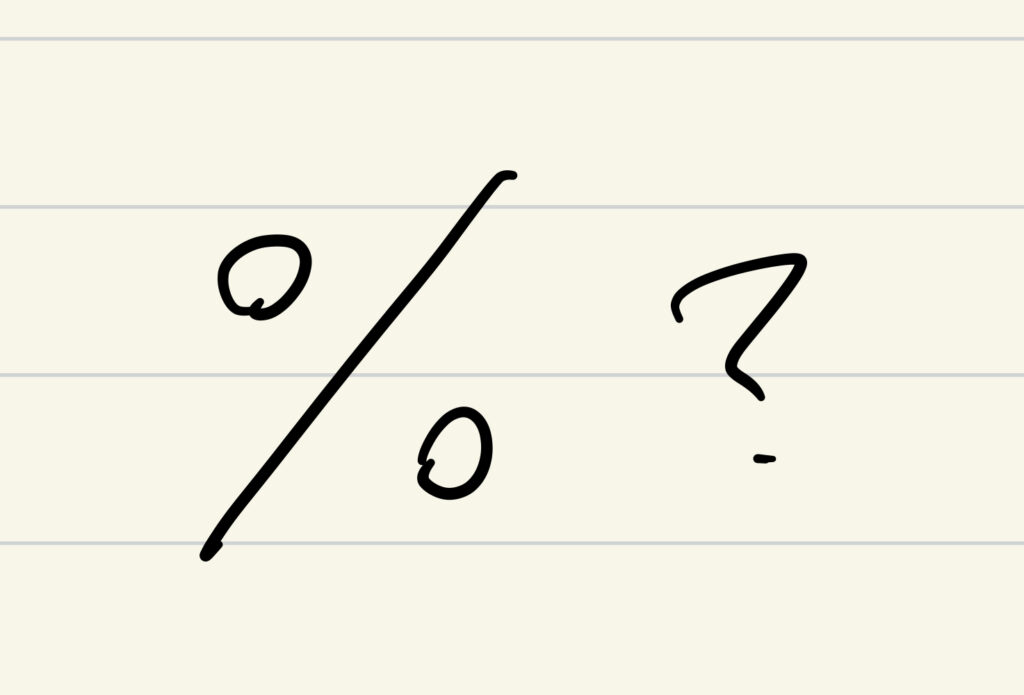
%は割合です。割合の問題はどういう問題があるでしょうか？

例えば先日のブログで書いた食塩水の問題。

あれは食塩水（g）の中にどれだけ食塩(g)が解けているか？という問題でした。

つまり同じ単位で割っているということになります。

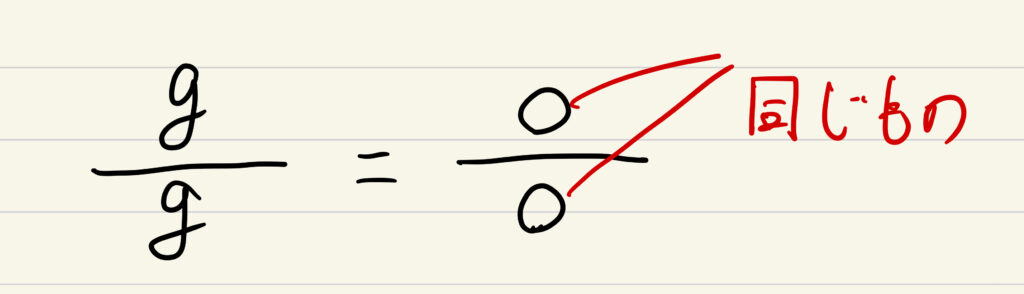
お団子が二つ並んでいるのは同じ単位で割りますよという意味だと覚えておけばわかりやすい。

ちなみにですが、何で割合で100をかける必要があるのかは、単純にわかりやすいからです。
全体を100とした時にどれくらいあるのか？というのは相手に伝えやすくイメージがしやすいのです。

単位一つでもただ先生から教えてもらうよりは、こういう豆知識や違う角度から知れると良いですよね。

僕がサラリーマンをしていた時、上司から「前向きな面倒くさがりは優秀」と言われていました。

ただ単にサボるというよりはどうせやらないといけないのなら、効率よくできる方法を探すアンテナが立っている人の方が優秀だという意味です。

僕自身も面倒くさがりなので、数学に関してもこの解答わかりにくいな〜もうちょっと楽に解けないかな〜とか常に考えていました。

その結果成績も自然に伸び、いろんな発見や気づきが生まれました。

面倒くさがりは長所です！笑

今日の解答#019